Table of Contents
Forecast tool CAPTRD
The tool providing projections for the European regions (the EU as of 2019, Turkey, Norway, Albania, Northern Macedonia, Montenegro, Bosnia and Herzegovina, Kosovo and Serbia) in CAPRI is called CAPTRD. It operates in several steps:
- Step 1 involves independent trends on all series, providing initial forecasts and statistics on the goodness of fit or indirectly on the variability of the series.
- Step 2 imposes constraints like identities (e.g. production = area * yield) or technical bounds (like non-negativity or maximum yields) and introduces specific expert information given on the MS level.
- Step 3 includes expert information on aggregate EU markets, typically coming from the AgLink model or GLOBIOM. This external data is not available for all individual countries in CAPRI, but for larger regions. Therefore, several countries must be simultaneously estimated in order to ensure proper use of this important prior information.
- Step 4 Depending on the aggregation level chosen the MS result may be disaggregated in subsequent steps to the regional level (NUTS2) or even to the level of farm types.
The trends estimated in CAPTRD are subject to consistency restrictions in steps 2 and 3. Hence they are not independent forecasts for each time series and the resulting estimator is hence a system estimator under constraints (e.g. closed area and market balances). Nonetheless, the trends are mechanical in the sense that they respect technological relationships but do not include any information about behavioural functions or policy developments1).
CAPTRD results are in turn only the first of several steps before a full CAPRI baseline is ready to use. The rest of this chapter focuses on CAPTRD.
Step 1: Independent, weighted nonlinear least squares
Before entering into the details it should be stated that ultimately almost any projection may be reduced to a particular type of trend projections, at least if the exogenous inputs, such as population, prices or household expenditure are also projected (usually by other research teams) as functions of time. In this sense trend projection may provide a firm ground on which to build projections and this is exactly their purpose in our work.
The first ingredient in the estimator is the trend curve itself which is defined as:
\begin{equation} X_{r,i,t}^{j,Trend}=a_{r,i,j}+b_{r,i,j}t^{c_{r,i,j}} \end{equation}
where the parameters a, b and c are to be estimated so that the squared deviation between given and estimated data are minimized. The X stands for the data and represents a five dimensional array, spanning up products i and items j (as feed use or production), regions r, points in time t and different data status such as ‘Trend’ or ‘Observed’. The trend curve itself is a kind of Box-Cox transformation, as parameter c is used as the exponent of the trend. For c equal unity, the resulting curve is a straight line, for c between 0 and 1, the curve is concave from below, i.e. increasing but with decreasing rates, whereas for c > 1, the curve is convex from below, i.e. increasing with increasing rates. In order to prevent differences between time points to increase sharply over the projection period, the parameters c are restricted to be below 1.2.
This form has the advantage of ensuring monotonic developments whereas quadratic trends often gave increasing yields for the first part of the projection period and afterwards a decrease. Another conclusion from the early explorations was that it is useful to define the trend variable \(t_{1984} = 0.1, t_{1985} = 0.2, t_{1986} = 0.3 \) etc., giving a potentially strong nonlinearity in the early years of the database (where the frequency of high changes, possibly due to data weaknesses was high) and a rather low nonlinearity in the projection period.
The ex-post period usually covers the period from 1985 towards the end of the underlying CAPREG output (file res_time_series.gdx) which is typically 4-6 years before the current year. The national level COCO data may have somewhat longer series than the regional CAPREG data. To account for this different availability of ex post data the following sets should be distinguished:
- Expost: defined from the length of the series in CAPREG output res_time_series.gdx
- Exante: covering any sequence of intermediate result years up to the user specified final year2).
- ExanteD: Ex ante years with additional COCO1 data (assigned in ‘captrd\ load_coco1_data.gms’)
- ExpostT: Union of Expost and ExanteD = years with data for trend estimation
The estimator minimises the weighted sum of squares of errors using the trend variable as weights:
\begin{equation} wSSE_{r,i,j}=\sum_{expost} \left(X_{r,i,expost}^{j,"Data"}-a_{r,i,j}+b_{r,i,j}t_{expost}^{c_{r,i,j}}\right)^2t_{expost} \end{equation}
The weighting with the trend was introduced in the exploration phase based on the following considerations and experience. First of all, it reflects the fact that statistics from the early years (mid eighties) are often less reliable then those from later years. Secondly, even if they are reliable, older data will tend to contribute less useful information than more recent ones due to ongoing structural change. For this reason we have discarded any years before 1992 for the New MS, for example, but the data from the mid 90ies may nonetheless represent a situation of transition that should count less than the recent past. In technical terms the step 1 estimates are found by a grid search over selected values of parameter c with analytical OLS estimates for parameters a and b (see ‘captrd\estimate_trends.gms’) that have been found identical to those of the econometric package Eviews for a given value of c (holds also for wSSE).
Step 2.1: Consistency constraints in the trend projection tool
Step 2 adds the consistency conditions and thus transforms the naïve independent trends into a system estimator. In almost all cases, the unrestricted trend estimates from the first step would violate one or several of the consistency conditions. We want to find estimates that both fit into the consistency constraints and exploit the information comprised in the ex-post development in a technical feasible way. Consider the identity that defines production as hectares/herd sizes times yield. Running independent trend estimates for barley area, barley yield and barley production will almost certainly produce estimates where production is not equal to yield times area. One solution would be to drop one of the three estimates, say yield, and replace it instead by the division of forecasted production by forecasted area. However, by doing so, we throw away the information incorporated in the development of barley yield over time. Adding relations between time series hence helps us to exploit more information than is contained in single series.
When consolidating simultaneously the different Step1 estimates, we will minimise the squared deviations from values computed in Step 1, in the following called “supports”, while complying with all constraints. A risk is that shaky trends may give a forecast line with an end point far away from ex-post observations. Hence we need safeguards pulling our estimates to a ‘reasonable’ value in such cases.
The confidence interval from the Step 1 trend estimation will not help, as it will be centred around the last projection value and as it will simply be quite large in case of a bad R². However, we may use the idea underlying the usual test statistics for the parameters related to the trend (a,b,c). These statistics test the probability of (a,b,c) being significantly different from zero. It can be shown that these tests are directly related to R² of the regression. If the zero hypotheses would be true, i.e. if the estimated parameters would have a high probability of being zero, we would not use the trend line, but the mean of the series instead.
This reasoning is the basis for the supports derived from the Step 1 estimates in CAPTRD (‘captrd\define_stats_and_supports.gms’), after some modifications. First of all, we used a three-year average based on the last known values as the fallback position and not the mean of the series. Secondly, in typical econometric analysis, test statistics would only be reported for the final estimation layout, some variables would have been dropped from the regression beforehand if certain probability thresholds are undercut. For our applications, we opted for a continuous rule as the choice of threshold values is arbitrary. The smaller the weighted R² the stronger the estimates are drawn towards our H0 – the value is equal to the recent three year average:
\begin{equation} X_{r,i,exante}^{j,"Support"}=wR_{r,i,j}^2 \left( a_{r,i,j}+b{r,i,j}t_{exante}^{c_{r,i,j}}\right)+\left(1-wR_{r,i,j}^2\right)X_{r,i,bas}^{j,"Data"} \end{equation}
where \begin{equation} wR_{r,i,j}^2=1-wSSE_{r,i,j}/wSST_{r,i,j} \end{equation}
and the weighted total sum of squares is defined analogous to equation below: \begin{equation} wSST_{r,i,j}=\sum_{expost}\left(X_{r,i,expost}^{j,"Data"}-X_{r,i,wAve}^{j,"Data"}\right)^2t_{expost} \end{equation}
with a trend weighted average \begin{equation} X_{r,i,wAve}^{j,"Data"}=\sum_{expost}X_{r,i,expost}^{j,"Data"}\cdot t_{expost}/\sum_{expost}t_{expost} \end{equation}
How is this rule motivated? If R² for a certain time series is 100%, in other words: for a perfect fit, the restricted trend estimate is fully drawn towards the unrestricted Step 1 estimate. If R² is zero, the trend curve does not explain any of the weighted variance of the series. Consequently, the support is equal to the ‘base data’. The ‘base data’ represent a three-year average around the last three known years. For all cases in between, the supports are the weighted average of the unrestricted trend estimate weighted with R² and the three-year average weighted with (1-R²). Generally, all trend estimates are restricted to the non-negative domain.
The above definition of supports works for series with expost data from CAPREG only as well as for those series with an extended set of observations (expostT, see above). The only difference is whether the three year average denoted above simply with “bas” is calculated using the three last years from set expost or from set expostT (BASM or BAST in ‘captrd\define_stats_and_supports.gms’).
Our objective function for Step 2 will be the sum of squared deviations from the supports defined above, weighted with the variance of the error terms from the first step: \begin{equation} Penalty=\sum_{r,i,j,expost}\left(\frac {X_{r,i,exante}^{j,"Trend"}-X_{r,i,exante}^{j,"Support"}}{\sqrt X_{r,i,verErr}^{j,"Step1"}}\right)^2 \end{equation}
where the weighted variance of errors is \begin{equation} X_{r,i,verErr}^{j,"Step1"}=wSSE_{r,i,j}/\left(\sum_{expost}t_{expost} -1\right) \end{equation}
The variance of the error term is used to normalise the squared deviations from all series which serves two purposes. First the weighted error variance is decreasing with the mean of the explanatory variable. Normalizing with it will hence ensure that the penalty targets relative rather than absolute deviations. Otherwise the solver would only tackle the deviations from “large” crops, say soft wheat, and more or less ignore the deviations of oats, for example. Secondly the deviations from the support are penalized stronger where the Step 1 trend had a high explanatory power and therefore a low variance of the error term.
The constraints in the trend projection enforce mutual compatibility between baseline forecasts for individual series in the light of relations between these series, either based on definitions as ‘production equals yield times area’ or on technical relations between series as the balance between energy deliveries from feed use and energy requirements from the animal herds. The set of constraints is deemed to be exhaustive in the sense as any further restriction would either not add information or require data beyond those available. The underlying data set takes into account all agricultural activities and products according to the definition of the Economic Accounts for Agriculture.
The constraints discussed in the following (from ‘captrd\equations.gms’) can be seen as a minimum set of consistency conditions necessary for a projection of agricultural variables. The full projection tool features further constraints especially relating to price feedbacks on supply and demand.
Constraints relating to market balances and yields
Closed market balances (CAPTRD eq. MBAL_) define the first set of constraints and state that the sum of imports (IMPT) and production (GROF) must be equal to the sum of feed (FEDM) and seed (SEDM) use, human consumption (HCOM), processing (INDM,PRCM,BIOF), losses (LOSM) and exports (EXPT):
\begin{align} \begin{split} X_{r,i,t}^{IMPT,Trend}+X_{r,i,t}^{GROF,Trend}&=X_{r,i,t}^{FEDM,Trend}+X_{r,i,t}^{SEDM,Trend}+X_{r,i,t}^{PRCM,Trend}\\ &+X_{r,i,t}^{INDM,Trend}+X_{r,i,t}^{BIOF,Trend}+X_{r,i,t}^{LOSM,Trend} \\ &+X_{r,i,t}^{HCOM,Trend}+X_{r,i,t}^{EXPT,Trend} \end{split} \end{align}
Where r are the Member States of the EU, i are the products, t the different forecasting years, corresponding to the equation. In the case of secondary products (dairy products, oils and oilcakes, for example) production is given on item MAPR. Domestic use DOMM (sum of the right hand side without exports) and net trade NTRD are defined in separate equations (DOMM_, NTRD_) not reproduced here. They do not act as constraints but permit a link to expert projections for EU markets in Step 3.
Secondly, production of agricultural raw products (GROF) is equal to yield times area/herd size (LEVL) where acts are all production activities (eq. GROF_):
\begin{equation} X_{r,i,t}^{GROF,Trend}= \sum_{acts}X_{r,i,t}^{acts,Trend}X_{r,LEVL,t}^{acts,Trend} \end{equation}
The market balance positions for certain products enter adding up equations for groups of products (cereals, oilseeds, industrial crops, vegetables, fresh fruits, fodder production, meat, eq. MBALGRP_). As an example, total cereal production is equal to the sum over the produced quantities of the individual cereals.
\begin{equation} X_{r,pro\_grp,t}^{MrkBal,Trend}= \sum_{i\in pro\_grp}X_{r,i,t}^{MrkBal,Trend} \end{equation}
Constraints relating to land use and cropping area
Adding up over the individual crop areas defines the total utilizable agricultural area (UAAR,LEVL, AREAB_):
\begin{equation} X_{r,LEVL,t}^{UAAR,Trend}= \sum_{crops}X_{r,LEVL,t}^{crops,Trend} \end{equation}
Adding up over the individual crop areas defines (in GRPLEVL_) the level of groups (set GrpC = {cereals, oilseeds, industrial crops, vegetables, fresh fruits, fodder production on arable land}):
\begin{equation} X_{r,LEVL,t}^{GrpC,Trend}= \sum_{crops \in GrpC}X_{r,LEVL,t}^{crops,Trend} \end{equation}
Adding up over mutually exclusive land use (in LANDUSEB_, for set LandUseARTO, see Annex: Tables 7-9) defines the total area (ARTO,LEVL):
\begin{equation} X_{r,LEVL,t}^{ARTO,Trend}= \sum_{LandUseARTO}X_{r,LEVL,t}^{LandUseARTO,Trend} \end{equation}
Constraints relating to agricultural production
Another Equation (OYANI_) links the different animal activities over young animal markets:
\begin{equation} X_{r,oyani,t}^{GROF,Trend}-X_{r,oyani,t}^{STCM,Trend}= \sum_{iyani\leftrightarrow oynai}X_{r,iyani,t}^{GROF,Trend} \end{equation}
Where oyani stands for the different young animals defined as outputs (young cows, young bulls, young heifers, male/female calves, piglets, lambs and chicken). These outputs are produced by raising processes, and apart from stock changes STCM (defined in Equation SOYANI_, not reproduced here), they are completely used as inputs in the other animal processes (fattening, raising or milk producing).
For those activites that have been split up in the database into a high and low yielding variant (DCOW, BULF, HEIF, GRAS) with 50% for each, this split is maintained (SPLITFIX_)
\begin{equation} X_{r,LEVL,t}^{splitactlo,Trend}= X_{r,LEVL,t}^{splitacthi,Trend} \end{equation}
The purpose of this split has been to permit an endogenous variation of yields also for animal activites, but so far no statistical information on the distribution of intensities has been available. Hence “intensive” has been defined to represent the upper 50% of the total distribution and it makes sense to maintain this split also in the baseline.
Animal herds (HERD) are related to animal activity levels through the process length in days (DAYS) via HERD_.
\begin{equation} X_{r,HERD,t}^{maact,Trend}= X_{r,LEVL,t}^{maact,Trend}\cdot X_{r,DAZS,t}^{maact,Trend} /365 \end{equation}
The process length is fixed to 365 days for female breeding animals (activities DCOL, DCOH, SCOW, SOWS, SHGM, HENS) such that the activity level is equal to the herd size3). For fattening activites the process length, net of any empty days (relevant for seasonal sheep fattening in Ireland, for example) times the daily growth should give the final weight after conversion into live weight with the carcass share carcassSh and consideration of any starting weight startWgt in FinalWgt_
\begin{align} \begin{split} X_{r,yield,t}^{maact,Trend}/carcassSh_{maact}=&startWgt_{maact}+X_{r,DAILY,t}^{maact,Trend}\\ &\cdot (X_{r,DAYS,t}^{maact,Trend}-X_{r,EDAYS,BAS}^{maact,data}) \end{split} \end{align}
As the daily growth is an important input into the livestock sector requirement functions it turned out useful to explicitely link it to the yields in terms of meat, both in the expost data (accounting identities in COCO) and here in the projections. Heavier animals require in this way a higher daily growth and/or a longer fattening period. For all inputs into the requirement functions hard constraints have been imposed (without the possibility to relax them in the solution process) to ensure that projected variables are fully in line with these contraints, mostly over bounds in ‘estimate_MS.gms’, but also through a specific (ad hoc) equation for male adult cattle that permits at most a daily growth of 0.4+500*0.0016 = 1.2 kg per day for a 500 kg final live weight, but more for heavier animals (DAILYUP_).
\begin{equation} X_{r,DAILY,t}^{bulf,Trend}\lt 0.4 + X_{r,meat,t}^{bulf,Trend}/carcassSh_{maact}\cdot 0.0016 \end{equation}
While all information for the requirement functions of CAPRI is projected consistently, they are not active in their detailed form in CAPTRD due to the complexity of the respective calculations. Instead these requirement functions are included in a simplified form as part of the balances for energy and protein requirements (REQS_) for each animal type maact:
\begin{equation} \sum_{feed}X_{r,feed,t}^{maact,Trend}X_{r,feed,t}^{Cont,Trend}= 0.998^t(a_{maact}^{Const}+a_{maact}^{Slope} X_{r,yield,t}^{maact,Trend}) \end{equation}
where Cont are the contents in terms of energy and crude protein. The left hand side of the equation defines total delivery of energy or protein from the current feeding practise per animal activity in region r, whereas the right hand side the need per animal derived from requirement functions depending on the main output (meat, milk, eggs, piglets born). The parameters a and b of the requirement functions are estimated from engineering functions as implemented in the CAPRI modelling system, and scaled so that the balance holds for the base year. The factor in front of the requirements introduces some input saving technical progress of -0.2% per annum.
The feeding coefficients multiplied with the herd sizes define total feed use for the different feeding stuffs ‘bulks’ (cereals, protein rich, energy rich, dairy based, other) and single nontradable feed items (grass, maize silage, fodder root crops, straw, milk for feeding, other fodder from arable land), technically in the same (GROF_) equation as equation below:
\begin{equation} X_{r,feed,t}^{GROF,Trend}=\sum_{maact}X_{r,feed,t}^{maact,Trend}X_{r,levl,t}^{maact,Trend} \end{equation}
Feed use of individual products must add up to the feed use of the ‘bulks’ mentioned above (in FEED_):
\begin{equation} X_{r,feed,t}^{FEDM,Trend}=\sum_{o\rightarrow feed}X_{r,o,t}^{FEDM,Trend} \end{equation}
Additional equations impose that certain stable relationships of agricultural technology are also maintained in projections:
- Equation EFED_ ensures that feed use of non-tradable fodder items must be equal to production after accounting for losses.
- Other equations (PosLo_, PosUp_) force the relation of seed use or losses to production (plus imports for losses) into a +-20% range around the base year value.
- Production has to exceed seed use and losses (SEED_)
- The ratio of straw to cereal yields is maintained at base year values (STRA_)
- Livestock units per hectare are calculated (LU_) and may thus be subject to constraints (limiting their deviations from the supports, for example).
Finally there is an Equation (LABO_) ensuring that projections of family (LABH) and hired labour (LABN) in agriculture add up to total labour (LABO):
\begin{equation} X_{r,LABO,t}^{GROF,Trend}=X_{r,LABH,t}^{GROF,Trend}X_{r,LABN,t}^{GROF,Trend} \end{equation}
In the first place projections of family and hired labour follow from input coefficients combined with the activity levels, but the previous equation permits to apply bounds to the total.
Constraints relating to prices, production values and revenues
The check of external forecasts revealed that for some products, external price projections are not available. It was decided to include prices, value and revenues per activity in the constrained estimation process. The first Equation (EAAG_) defines the value (EAAG, position from the Economic Accounts for Agriculture) of each product and product group as the product of production (GROF) times the unit value prices (UVAG):
\begin{equation} X_{r,i,t}^{EAAG,Trend}=X_{r,i,t}^{GROF,Trend}X_{r,i,t}^{UVAG,Trend} \end{equation}
The revenues of the activities (TOOU, total output) for each activity and group of activities acts are defined in Equation REVE_ as:
\begin{equation} X_{r,TOOU,t}^{acts,Trend}=\sum_o X_{r,o,t}^{acts,Trend}X_{r,o,t}^{UVAG,Trend} \end{equation}
Consumer prices (UVAD) are equal to producer prices (UVAG) plus a margin (CSSP ) according to Equation UVAD_: 4) 
\begin{equation} X_{r,i,t}^{UVAD,Trend}=X_{r,i,t}^{UVAG,Trend}X_{r,i,t}^{CMRG,Trend} \end{equation}
Constraints relating to consumer behaviour
Human consumption (HCOM) is defined as per head consumption multiplied with population (HCOM_):
\begin{equation} X_{r,i,t}^{HCOM,Trend}=X_{r,i,t}^{INHA,Trend}X_{r,LEVL,t}^{INHA,Trend} \end{equation}
Consumer expenditures per caput (EXPE) are equal (via EXPE_) to human consumption per caput (INHA) times consumer prices (UVAD):
\begin{equation} X_{r,i,t}^{EXPE,Trend}=X_{r,i,t}^{INHA,Trend}X_{r,LEVL,t}^{UVAD,Trend} \end{equation}
Total per caput expenditure (EXPE.LEVL) must add up (in Equation EXPETOT_):
\begin{equation} X_{r,LEVL,t}^{EXPE,Trend}=\sum_i X_{r,i,t}^{ESPE,Trend} \end{equation}
Constraints relating to processed products
Marketable production (MAPR) of secondary products (sec) - cakes and oils from oilseeds, molasses and sugar, rice and starch - is linked in Equation MAPR_ to processing of primary products (PRCM) by processing yields (PRCY):
\begin{equation} X_{r,sec,t}^{MAPR,Trend}=\sum_{i \wedge sec \leftarrow i} X_{r,i,t}^{PRCM,Trend}X_{r,sec,t}^{PRCY,Trend} \end{equation}
In case of products from derived milk (mlkseco) – butter, skimmed milk powder, cheese, fresh milk products, cream, concentrated milk, whole milk powder whey powder, and casein – eq. MLKCNT_ requires that fat and protein content (MLKCNT) of the processed raw milk (MILK5)) be equal to the content of the derived products, after acknowlegding that small quantities of dairy products are themselves transformed to other dairy products (most relevant for processed cheese):
\begin{equation} X_{r,MILK,t}^{PRCM,Trend}X_{r,MILK,t}^{MLKCNT,Trend}=\sum_{mlk\, sec\, o} \left( X_{r,mlk\, sec\, o,t}^{MAPR,Trend} X_{r,mlk\, sec\, o,t}^{PRCM,Trend}\right) X_{r,mlk\, sec\, o,t}^{MLKCNT,Trend} \end{equation}
Marketable production of by-products from the brewery, milling and sugar industry (set RESIMP = { FENI, FPRI}) are derived from corresponding uses of related products (cereals and sugar, Equation MaprByFeed_):
\begin{align} \begin{split} X_{r,resimp,t}^{MAPR,Trend}= & \sum_{o \rightarrow resimp} \left(X_{r,o,t}^{HCOM,Trend} +X_{r,o,t}^{PRCM,Trend} +X_{r,o,t}^{INDM,Trend} +X_{r,o,t}^{BIOF,Trend}\right) \\ & \cdot \frac {X_{r,resimp,t}^{MAPR,bas}}{ \sum_{o \rightarrow resimp} \left( X_{r,o,t}^{HCOM,bas} +X_{r,o,t}^{PRCM,bas}+ X_{r,o,t}^{INDM,bas}+ X_{r,o,t}^{BIOF,bas}\right)} \end{split} \end{align}
Constraints relating to bio-fuel production
Marketable production (MAPR) of biofuels (seco_biof) derives (according to Equation BIOF_) from non agricultural production NAGR (e.g biodiesel from waste oil), from second generation production SECG , or through processing yields in terms of biofuels 6) (PRCB) from biofuel use of first generation feedstocks (BIOF):
\begin{equation} X_{r,seco\_biof,t}^{MAPR,Trend}=\sum_{stocks \rightarrow seco\_biof } X_{r,stocks,t}^{BIOF,Trend} X_{r,stocks,t}^{PRCB,Trend} \end{equation}
In case of ethanol there is another by-product, DDGS, which is usable as a feedstuff and produced according to by-product coefficients from cereals (DDGS_):
\begin{equation} X_{r,DDGS,t}^{MAPR,Trend}=\sum_{stocks \rightarrow DDGS} X_{r,stocks,t}^{BIOF,Trend} X_{r,stocks,t}^{PRCBY,Trend} \end{equation}
Constraints relating to policy
There are only a few constraints directly taken from an EU regulation: firstly, the acreage under compulsatory set-aside (abolished in the CAP Health Check of 2008) must be equal to the set-aside obligations of the individual crops (OSET_):
\begin{equation} X_{r,"levl",t}^{"OSET",Trend}=\sum_{cact} X_{r,"levl",t}^{cact,Trend} \frac {0.01 X_{r,"setr",t}^{cact,Trend}}{\left(1-0.01X_{r,"setr",t}^{cact,Trend}\right)} \end{equation}
Secondly, we have the quota products milk and sugar. The milk quotas on deliveries are acknowledged with a fixing on processing of cow milk without an explicit equation, taking into account that there are countries with persistent under- or over-deliveries. Given the expiry of milk quotas after 2015 this is largely irrelevant for current applications of CAPTRD. The sugar quotas, by contrast, are included as an upper bound (SugaQuot_) that may be relaxed (see Regulation 318/2006, Article 12) through industrial or biofuel use of sugar (and losses of sugar):
\begin{equation} X_{r,SUGA,t}^{MAPR,Trend} \le X_{r,SUGA,t}^{QUTS,Trend}+ X_{r,SUGA,t}^{INDM,Trend}+ X_{r,SUGA,t}^{BIOF,Trend}+ X_{r,SUGA,t}^{LOSM,Trend} \end{equation}
Finally, there are upper bounds on new plantings of vineyards according to the CMO for wine from Regulation 1493/1999
Constraints relating to growth rates
During estimation, a number of safeguards regarding the size of the implicit growth rates had been introduced in the course of various past CAPRI projects (bounds mainly found in ‘captrd\fix_est.gms’):
- In general, input or output coefficients (yields) are not allowed to change by more than +/- 2.5 % per annum, with a higher ranges for feed input coefficients (+/- 10 % and +/ 5 % for non-marketable fodder).
- The number of calves born per cow is may only change up to +/- 10 % around the base period value until the last projection year.
- The number of young cows (or sows) needed for replacement may only change up to +/ 20 % around the base period value until the last projection year.
- Final fattening weights must fall into a corridor of +/- 20% around the base period value.
- Milk yields are assumed to increase at least by 0.25% and at most by 1.25% near the EU average with some correction for below or above average initial yields (in ‘captrd\comibounds.gms’).
- Crop yields (except those of very hererogeneous crops like “other fruits” or “other fodder on arable land) should have a minimum yield growth of 0.5%.
- Specific (and quite generous) upper limits are applied to prevent unrealistic crop yields (for example: 15 tons/ha for cereals)
- Technical coefficients like contents of milk products or processing yields are also subject to plausible bounds.
- Strong increases in pork and poultry production in the past are restricted by environmental legislation in force, notably the nitrate directive. Accordingly, yearly increases were restricted to +1% for pork in EU15 Member States (even more stringent for Denmark and The Netherlands) and to 1.5% for poultry. In the new MS these maximum growth rates are assumed to be half a percentage point larger, in line with a weaker implementation of environmental legislation. The same bounds are also applied to the corresponding activity levels.
- A strong decrease of animal activity levels (below 20% of the base year) is not allowed.
- Total agricultural area is not allowed to decline at a rate exceeding -0.2 % per annum.
- Shares of arable crop on total arable area are bounded by a formula which allows small shares to expand or shrink more compared to crops with a high share. A crop with a base year share of 0.1% is allowed to expand to 2.5%, one of 10% only to 25%, and one of 50% to only 70%:
\begin{align} \begin{split} X_{r,"levl",t}^{arab,Trend} .up / lo = & X_{r,"levl",bas}^{arab,Trend} \\ & \pm 1/4 \left( \frac {X_{r,"levl",bas}^{arab,Trend}} {X_{r,"levl",bas}^{"arab",Trend}} \right)^{1/4} X_{r,"levl",bas}^{"arab",Trend} \; max\left(0.2,\frac {t-bas} {last-bas} \right) \end{split} \end{align}
- However, in line with cross-compliance constraints from the CAP, permanent grass land must not decrease by more than 10% compared to the base year.
- An upper bound of 1% applies to the yearly growth of the area of “other oils” (for unclear reasons)
- Total labour must not deviate by more than 5% from forecasts based on coefficients estimated in an earlier study (“CAPRI-DYNASPAT”).
- Changes in human consumption per caput for each of the products cannot exceed a growth rate of +/- 2% per annum. Due to some strong and rather implausible trends for total meat and total cereals consumption, the growth rate was restricted to +/- 0.8 % per annum for meat and +/- 0.4% per annum for cereals assuming that trend shifts between single items are more likely than strong trends in aggregate food groups.
- A downward sloping corridor is defined for subsistence consumption of raw milk (in ‘captrd\comibounds.gms’).
- Changes in prices are not allowed to exceed a growth rate of +/- 2% per annum, usually.
- Expert supports for biofuel related variables are given high priority with mostly tight corridors around these supports (in ‘captrd\biobounds.gms’).
- If a variable has dropped to zero according to recent COCO data it will be fixed to zero.
Step 2.2: Integration of specific expert support (Member State level or lower)
The definition of expert “supports” allows for provision of a mean and a standard deviation for all elements, and it is particularly useful for items for which the AgLink forcasts in step 3 are missing, or where there are other reasons for stability problems, such as missing historical data or very short time series
The expert supports are dealt with in ’captrd\expert_support.gms’. Currently, mainly three sources can be distinguished:
- Support for the development of the sugar and sugar beet sectors, evolved from a small study with the seed production company KWS
- Expert on the development of bio-fuel production (bio-ethanol, bio-diesel), and the input demand for the related feedstocks, mainly based on results from the PRIMES model
- Expert supports for some key time series impacting on GHG emission for some Member States provided by the EC4MACS projects
The standard deviation is expressed by a “trust level” between 1 and 10.
The following table presents selected results related to the EU27 biomass feedstock for bioenergy production from the PRIMES7)) biomass component (also given for each MS):
Table 22: Selected results related to the EU27 biomass feedstock for bioenergy production from the PRIMES biomass component
| Unit: ktoe (unless specified otherwise) | 2000 | 2005 | 2010 |
|---|---|---|---|
| Domestic Production of Biomass Feedstock | 69,087 | 87,595 | 101,303 |
| Crops | 1,228 | 5,419 | 12,500 |
| - Wheat | 0 | 601 | 2,462 |
| - Sugarbeet | 0 | 1,291 | 4,518 |
| - Sunflower/Rapeseed | 1,228 | 3,527 | 5,520 |
| - Lign. Crops | 0 | 0 | 0 |
| Agricultural Residues | 4,194 | 6,428 | 7,200 |
| Waste | 19,990 | 26,002 | 28,054 |
| Net imports of Biomass Feedstock | 239 | 1,598 | 4,289 |
| Pure Vegetable Oil as feedstock for bioenergy production | 239 | 1,598 | 4,289 |
| Cultivated Land (Kha) | 896 | 3,022 | 5,422 |
| Starch crops | 0 | 320 | 1,218 |
| Oil crops | 896 | 2,654 | 4,031 |
| Sugar Crops | 0 | 48 | 172 |
| Lignocellulosic crops | 0 | 0 | 0 |
The above information on the biomass production is NOT used as the immediate input for CAPRI for several reasons. Converting from ktoe to 1000 tons (using 0.37 ktoe/1000t for cereals, 0.05 ktoe/1000t for sugar beet, 0.52 ktoe/1000t for rape seed) gives the production for the bio-fuel sector which matches with the market position “BIOF” = processing to biofuels. For cereals we have indeed 6.7 million tons from PRIMES in 2010 and 7.0 million tons according to CAPRI. For oilseeds we have to convert the PRIMES information in terms of oilseeds into a quantity of vegetable oil, giving approximately 5.5 mtoe / 0.52 ktoe/1000t * 0.4 [rape oil/ rape seed] = 4.2 million tons which is considerably larger than the results from CAPRI8) 1.8 million tons. A similar comparison for the sugar sector may point at conversion problems with the units. The PRIMES sugar beet production should correspond to a sugar quantity of 4.5 mtoe / 0.05 ktoe/1000t * 0.15 [sugar/sugar beet] = 13.5 million tons of sugar equivalents which is close to the total sugar production in CAPRI of 15.7 million tons. Apart from these unresolved differences in the ex post data the main reason for NOT using these biomass production quantities from PRIMES is conceptual: They are given from supply functions specific to the bio-fuel sector whereas CAPRI covers the whole production (mostly for food purposes) such that the use of exogenous information for parts of the total may create problems for the CAPRI market balances.
A similar consideration also applies to the area information from PRIMES which refers to the specific areas used for biofuel purposes, except for the area for lignocellulosic crops.
Basically, the information “close” to agriculture (feed stock use and required areas) has not been taken from PRIMES assuming that it is preferable to estimate those in the context of the agricultural sector model CAPRI. On the other hand, the information on the production of bioenergy, including its main technologies and pathways, was supposed to be given reliably from the PRIMES biomass component exactly because it covers beyond agriculture also forestry and various forms of waste. The next table focuses on those results that will be used as the immediate inputs for CAPRI (thus omitting bio-energy from forestry, for example).
First of all PRIMES offers net imports, production and demand quantities for the biofuels itself. Production of biodiesel is split up according to the technology in first generation and second generation technologies (FT diesel, HTU diesel, pyrolysis diesel). For ethanol such a breakdown is not given in terms of production volumes, but the PRIMES output includes among the installed capacities also those for fermentation of sugar crops, starchy crops and lignocellulosic crops, the latter identifying the share for second generation production of ethanol. The input for first generation production of biodiesel (through esterification) is “bioheavy” which includes pure vegetable oil from domestic production, but also from various forms of waste oil (recovered oils, biocrude, pyrolysis oil). In addition the market balance for bioheavy includes imports (pure vegetable oil, the larger part according to the previous table for biodiesel production, a smaller part for direct use as fuel) and demand quantities of bioheavy. These are the key inputs for CAPRI, plus the area of lignocellulosic crops that is also a direct input to CAPRI.
In addition, there is more information that may be used in the future. Biogas production is mainly based on sewage systems but in part it also relies on animal manure (whereas the German particularity of biogas from green maize is not yet included). Biogas production from manure might be coordinated between PRIMES and CAPRI in the future. Equally the PRIMES assumptions on the amount of crop residues usable for bio-energy are not yet cross-checked with CAPRI. Finally, it should be mentioned that the use of waste in the PRIMES tables refers to other sources of bioenergy (like municipal waste).
Table 23: Results on biofules of PRIMES model
| Unit: ktoe (unless specified otherwise) | 2000 | 2005 | 2010 |
|---|---|---|---|
| Net imports of Bioenergy | 400 | 1,731 | 5,820 |
| Biodiesel | 0 | 0 | 1,948 |
| Bioethanol | 0 | 20 | 1,130 |
| Pure Vegetable Oil | 8 | 390 | 505 |
| Bioenergy Production | 67,971 | 84,554 | 95,430 |
| Biodiesel | 610 | 2,548 | 6,578 |
| - Biodiesel (1st gen.) | 610 | 2,548 | 6,578 |
| - FT diesel | 0 | 0 | 0 |
| - HTU diesel | 0 | 0 | 0 |
| - Pyrolysis diesel | 0 | 0 | 0 |
| Bioethanol | 0 | 561 | 2,193 |
| BioHeavy | 1 | 83 | 605 |
| - Recovered Oils | 0 | 43 | 589 |
| - Pure Vegetable Oil | 1 | 40 | 15 |
| - BioCrude | 0 | 0 | 0 |
| - Pyrolysis oil | 0 | 0 | 0 |
| BioGas | 352 | 871 | 2,049 |
| - Bio-gas | 352 | 871 | 2,049 |
| - Synthetic Natural Gas | 0 | 0 | 0 |
| Waste Solid | 12,353 | 13,985 | 14,654 |
| Waste Gas | 1,898 | 3,537 | 4,538 |
| Demand | 68,372 | 86,285 | 101,250 |
| Biodiesel | 610 | 2,548 | 8,526 |
| Bioethanol | 0 | 581 | 3,234 |
| BioKerosene | 0 | 0 | 0 |
| BioHydrogen | 0 | 0 | 0 |
| BioHeavy | 9 | 473 | 1,110 |
| BioGas | 352 | 871 | 2,049 |
| Waste Solid | 12,353 | 13,985 | 14,654 |
| Waste Gas | 1,898 | 3,537 | 4,538 |
| Capacities (Ktoe/yr) | 10,440 | 16,067 | 26,754 |
| Fermentation | 134 | 1,127 | 4,104 |
| - Sugar | 0 | 551 | 2,103 |
| - Starch | 134 | 576 | 2,001 |
| - Lignocellulosic | 0 | 0 | 0 |
| Esterification | 1,141 | 4,170 | 9,021 |
In technical terms the PRIMES results are given as a set of Excel tables that is usually amended with each release in some detail. To extract these data a small GAMS program (‘merge.gms’) prepares strings that, when saved and reload with Excel, are interpreted as external links to the PRIMES files using the “Vlookup” function of Excel. The relevant data are written to a parameter p_PRIMESresults, including the following:
P_PRIMESresults(MS,BIOEshare,SECG,year)
= capacity, lignocellulosic / capacity fermentation
Otherwise the selection addresses directly certain lines of the PRIMES output.
Step 3: Adding comprehensive sets of supports from AGLINK or other agencies
In Step 3, results from external projections on market balance positions (production, consumption, net trade etc.) and on activity levels for EU aggregates (EU15, EU12) are added. Currently, these projections are provided by Aglink-COSIMO model projections. The baseline of Aglink-COSIMO integrates the market outlook results from DG-AGRI, but is also globally harmonised, so that it also enters the baseline generation for the market model of CAPRI.
Integration of results from another modelling system is a challenging exercise as neither data nor definitions of products and market balance positions are fully harmonized. That holds especially for Aglink-COSIMO, where at least in the past the mnemonics had even not been harmonized across equations of the model itself. After a restructuring exercise in 2010, that had somewhat been improved. The ingredients in the mapping process are first a list of the codes for the regions, products and items used in Aglink-COSIMO (‘baseline\aglink*_sets.gms’, where * can be 2009 or 2010 to differentiate the versions before and after the restructuring). A second program, (‘baseline\aglink*_mappings.gms’) links the CAPRI regions, products and items to the mnemonics and Aglink-COSIMO, and a larger program (‘baseline\loag_aglink*.gms’) then uses the mapping to assign them to the CAPRI code world.
Aglink-COSIMO currently features results at EU15 and EU12 level. It is hence not possible to funnel the Aglink-COSIMO results into Step 2 above without an assumption of the share of the individual Member States.
As DG-AGRI is often the main client of the CAPRI projections for the EU, it was deemed sensible to pull the projections towards the DG-AGRI baseline wherever the constraints of the estimation problem and potentially conflicting other expert sources allow for it. That is achieved by two assignments related to the objective function:
- Step 2 results (except those steered by other expert supports) are scaled proportionally to give MS level supports for step 3 that are consistent with the Aglink-COSIMO baseline (after adjusting for different definitions in the respective databases).
- The standard errors from the default trends are replaced with a special formula reflecting a high confidence in the Aglink-COSIMO derived supports.
More precisely, the weighted variance is replaced with the following setting for external supports (“XSupport” = AGLINK or expert supports):
\begin{equation} X_{r,i,"varErr"}^{j,"XSupport"}=\left(X_{r,i,"exante"}^{j,"XSupport"}\cdot 0.05/3 \cdot \left(10/X_{r,i,"trustlevl"}^{j,"XSupport"}\right)\right)^2 \end{equation}
The “trust level” in the last denominator is a scaling factor for the implied coefficient of variation. A higher trust level translates into a lower error variance of the external information. With a normal distribution we would have
- at “trust level” = 10: X ∈ [-0.055*Mean, +0.055*Mean] with probability 99.9%
- at “trust level” = 5: X ∈ [-0.275*Mean, +0.275*Mean] with probability 99.9%
- at “trust level” = 1: X ∈ [-0.55*Mean, +0.55*Mean] with probability 99.9%
The default setting for “DGAgri” supports is a “trust level” of 5, which is a moderately high value to leave some distance for special cases that should be pulled very tightly towards their supports.
The Aglink-COSIMO projections currently run to 2020 or a few years beyond. For climate related applications CAPRI has to tackle projections up to 2030 or even 2050. CAPRI projections up to 2030 have been prepared in the context of EC4MACS project (http://www.ec4macs.eu). The methodology was quite simple: The year 2020 projection (usually prepared in the same run of CAPTRD) has been extrapolated in a nonlinear dampened (logistic) fashion (in ‘define_eu_supports.gms’) with some additional bounds to prevent unreasonable increases of certain variables (nonnegativity already provided a good lower bound). Together with the information in the time series database this has been an ad hoc but operational procedure to address the 2030 horizon, but it would have been inappropriate for a move to the long run up to 2050 as required for a recent study on behalf of DG CLIMA9).
For the long run evolution of food production a link has been established to long run projections from two major agencies (FAO 2006 and the IMPACT projections in Rosegrant et al 2009, see also Rosegrant et al 2008). This linkage required mappings to bridge differences in definitions (see ‘gams\global\f2050_impact.gms’ called when running ‘gams\global.gms’).
Furthermore, methodology was needed to avoid a break in the projections at the transition of medium run expert information (Aglink-COSIMO, up to 2020) and long run information (FAO/IFPRI for 2050). For this purpose a variable weighting scheme is introduced (in ‘gams\captrd\expert_support.gms’) that gives an increasing weight to our “long run” sources (FAO/IFPRI) as the projection horizon approaches 2050. This tends to give projections that gradually approach the long run sources, for example as in the case of pork production in Hungary (taken from a baseline established in November 2011).
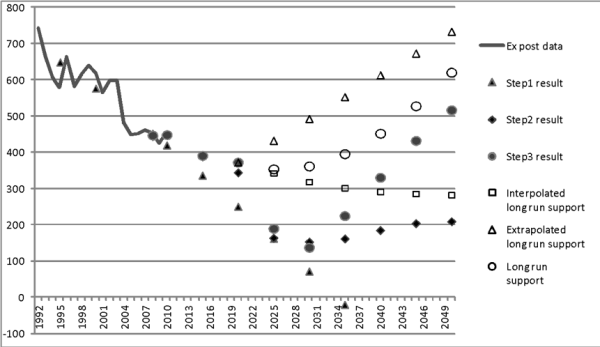
Figure 11: Pork production in Hungary as an example for merging medium run and long run a priori information in the CAPRI baseline approach
The example has been chosen because historical trends (and Aglink-COSIMO projections) on the one hand and long run expectations differ markedly. This is not unusual because medium run forecasts often give a stronger weight to recent production trends, often indicating a stagnating or declining production in the EU, whereas the long run studies tend to focus on the global growth of food demand in the coming decades. The simple trends (filled triangles) would evidently give unreasonable, even negative forecasts after 2030. Already the imposition of constraints from relationships to other series would stabilise the projections and imply some recovery after 2030 (filled squares). The year 2020 supports from Aglink-COSIMO (not shown) produces some upward correction of the step 2 results for 2020, giving a final projection (filled circles) of about 375 ktons for pork production in Hungary. This is also the starting point for the specification of the long run support (empty circles) which is a weighted average of two components. The first is a linear interpolation to the external projection from FAO/IFPRI for 2050 (empty triangles). The second is a nonlinear damped extrapolation of the medium run projection beyond 2020 (empty squares). Changing the weight for the first component (FAO/IFPRI support) with increasing projection horizon creates a long run target value (empty circles) that gives a smooth transition from the medium to the long run. As the final projections (filled circles) tend to follow these target values, they show a turning point in the future evolution of pork production in Hungary that ultimately reflects the consideration of increasing global demand underlying the FAO/IFPRI projections.
Evidently this approach is quite removed from economic modelling and it is not intended to be. Instead it tries to synthesize the existing projections from various agencies, each specialised in particular fields and time horizons, in a technically consistent and plausible manner. The specification of a constraint set and penalties of the objective function translates plausibility in an operational form. Technical consistency is imposed through the system of constraints active during the estimation.
Step 4: Breaking down results from Member State to regional and farm type level
Even if it would be preferable to add the regional dimension already during the estimation of the variables discussed above, the dimensionality of the problem renders such an approach infeasible. Instead, the step 3 projection results regarding activity levels and production quantities are taken as fixed and given, and are distributed to the regions minimizing deviation from regional supports. The aggregation conditions for this step (and correspondingly for the disaggregation of NUTS2 regions to farm types) are:
- Adding up of regional production to Member State production (MSGROF_)
- Adding up of regional agricultural and non-agricultural areas to Member State areas (eqs. MSLEVL_ and MSLANDUSE_)
- Adding up of regional feed use by animal types to Member State values (MSFEEDI_).
The results at Member State level are thus broken down to regional level, ensuring adding up of production, areas and feed use:
\begin{equation} X_{MS,i,t}^{GROF,Trend}=\sum_{r\in MS}X_{r,i,t}^{GROF,Trend} \end{equation}
\begin{equation} X_{MS,"levl",t}^{j,Trend}=\sum_{r\in MS}X_{r,"levl",t}^{j,Trend} \end{equation}
\begin{equation} X_{MS,"levl",t}^{j,Trend}\cdot \left(X_{MS,"feed",t}^{j,Trend}+10 \right)=\sum_{r\in MS}X_{r,"levl",t}^{j,Trend}\cdot \left(X_{r,"feed",t}^{j,Trend}+10 \right) \end{equation}
The addition of the “10” (kg/animal) considerably improves the scaling in case of very small quantities (say 1 gram per animal). This is an example of a technical detail that may be crucial for numerical stability but usually cannot be reported fully in this documentation.
In addition to the above aggregation conditions, the lower level (NUTS2 or farm type) models only require the following constraints (as the market variables are already determined at the MS level):
- Related to areas: area balance (Equation 57
), obligatory set aside (Equation 80
), aggregation to groups like cereals (0).
- Related to yields: linkage of production, activity levels and yields (Equation 55
), stabilisation of straw yields (STRA_)
- Related to animals: Nutrient balances (Equation 65
), local use of fodder (EFED_), definition of livestock density (LU_).
In order to keep developments at regional and national level comparable, relative changes in activity levels are not allowed to deviate very far from the national development. These bounds are widened in cases of infeasibilities.
Table below contains an example of the final output of the trends estimation task (C:\….CAPRI\STAR\star_2.4\output\results\baseline\results_BBYY.gdx), where BB stands for base year and YY for simulation year). Its main purpose is to provide with explanations on the variables of this output and, thus, a possibility to review the results in a step-by-step manner.
Table 24: Example of the final output of the trends estimation task and description of the variables
| Product code | Activity code | Variables | Years | Explanations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1984 | … | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | ||||
| SWHE | SWHE | BASM | 8337 | Base year value from Build database workstep. | ||||||||
| Penalty | 0.2 | “squared root” difference between actual estimate and support value. The larger the value, the farer the estimate from support. | ||||||||||
| Lo | 8080 | Lower estimation bound. | ||||||||||
| DGAgri1 | 8876 | 8385 | 8046 | 8109 | 8632 | 8996 | 9167 | Projection of Aglink-Cosimo for the EU15 aggregate scaled to fit the CAPRI database.10) | ||||
| TrustLevl | 3 | Exogeneous value used for restricting min and max values of the support values. It is used in calculating lower and upper bounds (up and lo) of the projections. | ||||||||||
| data | ||||||||||||
| BAST | 8579 | Simple average of the last 3 observation years available: 2012-2014. | ||||||||||
| B2000 | 7988 | |||||||||||
| support | 9167 | Values estimated as linear combination of Step1 and BAST (BASM) with R2 as weight. They are replaced with expert support where applicable and then scaled. They are then stored as Support1. Support is then redefined based on the Aglink-Cosimo value.11) | ||||||||||
| support1 | 8943 | (expert) support value, before introduction of Aglink-Cosimo calibration values. | ||||||||||
| step1 | 8918 | 1) Result of estimation of unconstrined trends | ||||||||||
| step2 | 8851 | 2) Results of solving the trend model with constraints at MS level and with support1 | ||||||||||
| step3 | 8949 | 3) First, it is defined as results of solving trend model with constraints at MS level and with support (defined with Aglink-Cosimo value). Then, it is redifined with the results from solving this trend model with additional constraints at NUTS2 level. | ||||||||||
| wVarErr | 259353 | |||||||||||
| CoefVarErr | 0.1 | |||||||||||
| Extrap | ||||||||||||
| Longrun | 8553 | 8579 | 8633 | |||||||||
| Longrun1 | ||||||||||||
| P_Data | 6975 | … | 9061 | 8614 | 8078 | 8139 | 8810 | 8789 | Historical data – output of Build database. The last observation year – 2014. | |||
| series | 6975 | … | 9061 | 8614 | 8078 | 8139 | 8810 | 8789 | 8949 | Historical values (until 2014) and projected values (starting from 2015 with 5-year step, as defined in the GUI setting for the Trends projection task). The projected values are “copied” from Step 3.12)13) | ||
| up | 8978 | Upper estimation bound | ||||||||||
Source: own compilation. Comments: SWHE in Product code column indicates soft wheat commodity. SWHE in Activity code indicates yield of soft wheat. The CAPRI model used for this example was calibrated to the projections of Aglink-Cosimo model.