This is an old revision of the document!
Table of Contents
Data Distribution Procedures
The terms spatial “resampling”, “re-mapping, “downscaling”, “disaggregation” and “distribution” are frequently used in a synonymous way. Admittedly, a very sharp distinction is sometimes difficult and there are overlaps in their meaning, this holds especially for “downscaling” and “disaggregation”. To avoid confusion of the reader we lay down our interpretation of these terms.
Resampling
By resampling we intend the process of interpolating from one grid resolution to a different grid resolution. Quantitative evaluation of data contained on different grids requires resampling to a common grid. There are many resampling methods. Classic interpolation methods include: bilinear, nearest neighbor, inverse distance. The consistency with the original dataset is not necessarily maintained.
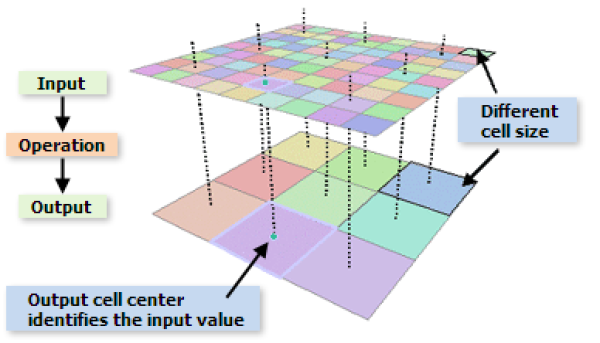
Example: Resampling of land use information at a regular grid of 100 x 100m from remote sensing to a 1km x 1km grid using the nearest neighbor method. The 1 x 1km grid receives the value of the 100 x 100 m grid which spatially coincides with the center of the 1 x 1km grid.
Sketch of the nearest neighbor interpolation method applied to a regular grid. (Source: ESRI ArcGIS documentation of resampling methods)
Re-mapping
In the context of this work we use the term re-mapping if the spatial reference unit of a given parameter has to be changed. The aim is to keep changes of the parameters/values at a minimum during the change of the spatial reference. Re-mapping is often required for pre- and post processing of data input/output of the downscaling/disaggregation/distribution procedures.
In the special case of nested data (i.e. a spatial unit at low hierarchical level is member of exactly one unit at a higher hierarchical level s. definition below) the re-mapping of values given at low hierarchical level to a higher hierarchical level can be obtained by simple aggregation (summing up or averaging). A typical example is the re-mapping of information given for administrative regions (NUTS3 - > NUTS2 → NUTS1 → NUTS0).
Definition of nested spatial reference data sets
\begin{equation} if \; 0 \lt a_{ij} \le 1 \; for\; i\in I \;and\; j\in J \; then\; a_{ik}=0 \;for \;i\in I \;and\; k\ne j \;and\; k\in J \end{equation}
More frequently data is stemming from various sources having different spatial reference units. For example meteo data which usually comes at a grid level (e.g. 50 x 50 km) and has to be re-mapped to an administrative unit. In these cases a spatial overlay of the data is performed and new spatial units are created at the intersection of the spatial units. In the meteo grid/administrative region case a meteo grid might be split by the border between 2 different administrative units.
To avoid creating very small spatial units during the re-mapping procedure we defined a minimum spatial unit of 1 x 1 km2 (i.e. the 1 by 1km EEA reference grid) as common denominator. All input data is rasterized or resampled to this unit before the re-mapping. For categorical data as e.g. land use/cover classes, the nearest neighbor interpolation method is applied. In other cases the share of the parameter in the 1 x 1 km2 grid is calculated (e.g forest area). After rasterizing/resampling of all data sets of interest, re-mapping of all parameters to any spatial reference unit present in the input data sets is possible.
Example: meteo data at 50 x 50 km grid level re-mapped to NUTS2 regions
Consistency of data between the rasterized versions of both spatial references is maintained:
\begin{equation} x_i=\frac{\sum_j x_j \cdot a_{ji}}{a_i} \end{equation}
I = units of the first layer (e.g. 50 km x 50 km grid)
J = units of the second layer (e.g. NUTS2 regions)
x = Area-based variable (e.g. average annual rainfall mm/m2; kg N/ha emissions; persons/ha; etc.)
a = Area. ai is the area of a unit of the layer the variable is re-mapped to. aij are the areas of the intersections between unit i and all units j that have common surface.
In case that \(\sum_j a_{ij} \le a_i\), that is there is a part of unit i which is not covered, assumptions on ‘gap-filling’ have to be made. Possible options are:
- Assuming same area-based variable thus giving higher total quantity
- Maintaining total quantity thus ‘diluting’ the area-based variable.
Increasing the spatial resolution of data for nested spatial references
We differentiate approaches for increasing the spatial resolution of data that are applicable to nested spatial data sets in view of the complexity of the approach. The complexity increases from simple distribution over downscaling to disaggregation.
Downscaling
As downscaling we understand a procedure to infer high-resolution information from low-resolution variables using simple proxy information that is available at the high resolution. Downscaling works only with nested spatial units. The consistency with the original dataset is maintained.
For example:
- downscaling population density in rural areas available at country level to a grid taking into account land cover information (rural areas/urban areas)
- downscaling of fertilizer input from national fertilizer use statistics based on distribution of crop yields available at higher spatial level (e.g. sub-national regions).
Disaggregation
Spatial disaggregation is the process by which information at a coarse spatial scale is translated to finer scales using weighting. The weights are based on more or less complex regression or other (optimization) models derived from observations, ancillary data, or previous downscaling/disaggregation steps. The consistency with the original dataset is maintained. One example is the use of LUCAS land use observations, environmental and management parameters to predict the probability of a crop to be cultivated at a certain location.
Simple Distribution
This procedure is applied if a parameter is available at high hierarchical level (e.g. country) and no information is available to enhance the spatial pattern for the lower hierarchical level (by proxies/regression/models) In this case, the spatial distribution of a parameter when changing the spatial reference unit from a higher to a lower hierarchical level is kept constant. Example: average nitrogen excretion rates for different livestock available at country level. A homogeneous distribution within all sub-units is assumed. Due to lacking information the effects of sub-national differences due to e.g. specific feeding strategies, are not taken into account.